3 Survival Analysis
This page is a work in progress and minor changes will be made over time.
Survival Analysis is concerned with data where the outcome is the time until an event takes place (a ‘time-to-event’). Because the collection of such data takes place in the temporal domain (it takes time to observe a duration), the event of interest is often unobservable, for example because it did not occur by the end of the data collection period. In survival analysis terminology this is referred to as censoring.
This chapter defines basic terminology and mathematical definitions in survival analysis, which are used throughout this book. Building upon this chapter, Chapter 4 introduces event-history analysis, which is a generalization to settings with multiple, potentially competing or recurrent events, including multi-state outcomes. Concluding this part of the book, Chapter 5 defines different prediction tasks in survival analysis.
While these definitions and concepts are not new to survival analysis, it is imperative they are understood to build successful models. Evaluation functions (Part II) can identify if one model is better suited than another to minimize a given objective function, however they cannot identify if the objective function itself was specified correctly, which depends on the assumptions about the data generating process. Evaluating models with the wrong objective function yields meaningless results. Hence, it is of utmost importance for machine learning practitioners to be able identify and specify the survival problem present in their data correctly to ensure models are correctly fit and evaluated.
3.1 Quantifying the Distribution of Event Times
This section introduces functions that can be used to fully characterize a probability distribution, particular focus is given to functions that are important in survival analysis.
Note that we can generally distinguish between events taking place in discrete time or continuous time. For example, consider the time a politician serves in parliament. If we consider the number of election cycles they stay in parliament, it would constitute discrete time, as time can only take values, \(1, 2, 3, \ldots\), that is \(Y\in \mathbb{N}_{>0}\). On the other hand, the time an individual stays in hospital is usually determined as the difference between the admission date-time and discharge date-time, which would constitute a continuous time \(Y\in \mathbb{R}_{\geq 0}\).
In practice the differences are often blurred as time-measurement will naturally be discretized at some level and precision beyond some resolution is often not of interest (hospital length of stay might be interesting up to days or hours, but not minutes and seconds). Also discrete-time methods are often applied to continuous time data and vice versa. It is nevertheless important to make the distinction as it informs mathematical treatment and definition of the different quantities introduced below.
3.1.1 Continuous Time
For now, assume a continuous, positive, random variable \(Y\) taking values in (t.v.i.) \(\mathbb{R}_{\geq 0}\). A standard representation of the distribution of \(Y\) is given by the probability density function (pdf), \(f_Y: \mathbb{R}_{\geq 0}\rightarrow \mathbb{R}_{\geq 0}\), and cumulative distribution function (cdf), \(F_Y: \mathbb{R}_{\geq 0}\rightarrow [0,1]; (\tau) \mapsto P(Y \leq \tau)\).
In survival analysis, it is more common to describe the distribution of event times \(Y\) via the survival function and hazard function (or hazard rate) rather than the pdf or cdf. The survival function is defined as \[ S_Y(\tau) = P(Y > \tau) = \int^\infty_\tau f_Y(u) \ \mathrm{d}u, \tag{3.1}\]
which is the probability that an event has not occurred by \(\tau \geq 0\) and thus the complement of the cdf: \(S_Y(\tau) = 1-F_Y(\tau)\). By definition, \(S_Y(0)=1\) and \(S(\tau)\rightarrow 0\) for \(\tau \rightarrow \infty\).
The hazard function is given by \[ \begin{aligned} h_Y(\tau) &= \lim_{\mathrm{d}\tau\searrow 0}\frac{P(\tau \leq Y < \tau + \mathrm{d}\tau|Y \geq \tau)}{\mathrm{d}\tau} \\ &= \lim_{\mathrm{d}\tau\searrow 0}\frac{P(Y \in [\tau, \tau + \mathrm{d}\tau)|Y \geq \tau)}{\mathrm{d}\tau}\\ & = \frac{f_Y(\tau)}{S_Y(\tau)} \end{aligned} \tag{3.2}\]
where \(\mathrm{d}\tau\) denotes a time-interval. The hazard rate is often interpreted as the instantaneous risk of observing an event at \(\tau\), given that the event has not been observed before \(\tau\). This is not a probability and \(h_Y\) can be greater than one.
The cumulative hazard function (chf) can be derived from the hazard function by \[ H_Y(\tau) = \int^\tau_0 h_Y(u) \ \mathrm{d}u, \tag{3.3}\]
and relates to the survival function via
\[ \begin{aligned} H_Y(\tau) & = \int^\tau_0 h_Y(u) \ \mathrm{d}u= \int^\tau_0 \frac{f_Y(u)}{S_Y(u)} \ \mathrm{d}u\\ & = \int^\tau_0 -\frac{S'_Y(u)}{S_Y(u)} \ \mathrm{d}u= -\log(S_Y(\tau)) \end{aligned} \]
These last relationships are particularly important, as many methods estimate the hazard rate, which is then used to calculate the cumulative hazard and survival probability \[ S_Y(\tau) = \exp(-H_Y(\tau)) = \exp\left(-\int_0^\tau h_Y(u)\ \mathrm{d}u\right) \tag{3.4}\]
Unless necessary to avoid confusion, subscripts are dropped from \(S_Y, h_Y\) etc. going forward and instead these functions are referred to as \(S\), \(h\) (and so on).
Usual regression techniques cannot be used to estimate these quantities as \(Y\) is only partially observed, due to different types of censoring and truncation (see Section 3.2, Section 3.3, Section 3.4).
3.1.2 Discrete Time
Now let \(\tilde{Y}\) be a discrete, positive random variable that represents discrete or discretized time, taking values in \(\mathbb{N}_{>0}\); and \(\tau\in \mathbb{N}_{>0}\) some time point in discrete time.
The discrete-time hazard rate is defined as
\[ h^d_{\tilde{Y}}(\tau) = P(\tilde{Y}=\tau|\tilde{Y} \geq \tau). \tag{3.5}\]
Thus, in contrast to the continuous time hazard 3.2, the discrete time hazard is an actual (conditional) probability, rather than a rate and therefore might be easier to interpret.
The cumulative discrete time hazard is given by
\[ H^d_{\tilde{Y}}(\tau) = \sum_{k=1}^{\tau}h^d_{\tilde{Y}}(k) \tag{3.6}\]
We also define the complement of 3.5, the probability to survive beyond \(\tau\) given survival until \(\tau\), as \[ s^d_{\tilde{Y}}(\tau) := 1 - h^d_{\tilde{Y}}(\tau) = P(\tilde{Y}> \tau|\tilde{Y} \geq \tau). \]
It follows that the unconditional probability to survive beyond time point \(\tau\) is given by
\[ S^d_{\tilde{Y}} = P(\tilde{Y} > \tau) = \prod_{k\leq\tau} s^d_{\tilde{Y}}(\tau) = \prod_{k\leq\tau}(1-h^d_{\tilde{Y}}(\tau)), \tag{3.7}\] and the unconditional probability for an event at time \(\tau\) is \[ P(\tilde{Y}=\tau) = S^d_{\tilde{Y}}(\tau-1) h^d_{\tilde{Y}}(\tau). \tag{3.8}\] When applied to continuous time \(Y\), the follow-up is divided in \(J\) disjunct intervals \((a_0,a_{1}],\ldots,(a_{j-1},a_j]\ldots, (a_{J-1},a_{J}],j=1,\ldots,J\) such that \[ Y \in (a_{j-1}, a_j]\Leftrightarrow \tilde{Y} = j \] Thus, \[ h^d_{\tilde{Y}}(j) = P(Y \in (a_{j-1},a_j]|Y > a_{j-1}) \]
and \[ S^d_{\tilde{Y}}(j) = P(Y > a_{j}) = S_Y(a_{j}) \]
For more details on discrete time-to-event analysis consider (Tutz and Schmid 2016).
3.2 Single-event, right-censored data
The complexity of Survival Analysis compared to other fields arises from the fact that the outcome of interest is often only observed partially. In particular, the time-to-event is often unknown at the end of the observation period, as the event has not occurred yet.
Let,
- \(X\) taking values in \(\mathbb{R}^p\) be the generative random variable representing the data features/covariates/independent variables.
- \(Y\) taking values in \(\mathbb{R}_{\geq 0}\) be the (partially unobservable) true survival time.
- \(C\) taking values in \(\mathbb{R}_{\geq 0}\) be the (partially unobservable) true censoring time.
In the presence of censoring \(C\), it is impossible to fully observe the true outcome of interest, \(Y\). Instead, the observable variables are defined by
- \(T := \min\{Y,C\}\), the outcome time (realizations are referred to as the observed outcome time); and
- \(\Delta := \mathbb{I}(Y = T) = \mathbb{I}(Y \leq C)\), the event indicator (also known as the censoring or status indicator).
Together \((T,\Delta)\) is referred to as the survival outcome or survival tuple and they form the dependent variables. The survival outcome provides a concise mechanism for representing the outcome time and indicating which outcome (event or censoring) took place.
A survival dataset is a \(n \times p\), real-valued matrix defined by \(\mathcal{D}= ((\mathbf{x}_1, \ t_1, \ \delta_1) \cdots (\mathbf{x}_n,t_n,\delta_n))^\top\), where \((t_i,\delta_i)\) are realizations of the respective random variables \((T_i, \Delta_i)\) and \(\mathbf{x}_i\) is a \(p\)-dimensional vector, \(\mathbf{x}_i = (x_{i;1} \ x_{i;2} \cdots x_{i;p})^\top\) of features.
In this book, we will often refer to the unique, ordered event times. For example, given survival data, \((t_1=6, \delta_1=0), (t_2=1, \delta_2=1), (t_3=10,\delta_3=1), (t_4=5,\delta_4=0), (t_5 =10,\delta_5=1)\) the ordered unique event times are \((t_{(1)}, t_{(2)}) = (1,10)\) as the censored observations are removed, as are duplicated times.
Let \(m\leq n\) be the number of unique, observed event times. We define the unique, ordered event times simply as
\[ t_{(1)}<\cdots<t_{(m)}, \qquad m\le n. \tag{3.9}\]
A common short-hand in survival analysis is to assume the subscript \((k)\) is an index referring to the observation who experienced the event at time \(t_{(k)}\). For example, \((\mathbf{x}_{(k)}, t_{(k)}, \delta_{(k)})\) are the features and outcome for the observation that experienced the event at \(t_{(k)}\), the \(k\)th ordered event time.
Finally, the following quantities are used frequently throughout this book and survival analysis literature more generally. Let \((t_i, \delta_i) \stackrel{i.i.d.}\sim(T,\Delta), i = 1,...,n\), be observed survival outcomes.
The risk set at \(\tau\), is the index-set of observation units at risk for the event just before \(\tau\)
\[ \mathcal{R}_\tau := \{i: t_i \geq \tau\} \tag{3.10}\]
where \(i\) is the index of an observation in the data. For right-censored data, \(\mathcal{R}_0 = \{1,\ldots,n\}\) and \(\mathcal{R}_{\tau} \subseteq \mathcal{R}_{\tau'}, \forall \tau > \tau'\). Note that in a continuous setting, ‘just before’ refers to an infinitesimally smaller time than \(\tau\), in practice, as this is unobservable the risk set is defined at \(\tau\), hence an observation may both be at risk, and experience an event (or be censored) at \(\tau\).
The number of observations at risk at \(\tau\) is the cardinality of the risk set at \(\tau\), \[ n_\tau := \sum_i \mathbb{I}(t_i \geq \tau) = |\mathcal{R}_\tau| \] Finally, the number of events at \(\tau\) is defined by, \[ d_\tau := \sum_i \mathbb{I}(t_i = \tau, \delta_i = 1) \] For truly continuous variables, one might expect only one event to occur at each observed event time: \(d_{t_{(k)}} = 1,\forall k\). In practice, ties are often observed due to finite measurement precision, such that \(d_{\tau} > 1\) occurs frequently in real-world datasets.
The quantities \(\mathcal{R}_\tau\), \(n_\tau\), and \(d_\tau\) underlie many models and measures in survival analysis. Several non-parametric and semi-parametric methods (Chapter 10) like the Kaplan-Meier estimator (see Section 3.5.2.1) are based on the ratio \(d_\tau / n_\tau\).
Table 3.1 exemplifies an observed survival dataset, a subset of the tumor data (Bender and Scheipl 2018), which contains the time until death in days after operation (\(\delta_i=1\) if death occurred at the outcome time \(t_i\) and \(\delta_i = 0\) otherwise).
In this example, the above quantities would be:
- \(\mathcal{R}_{\tau = 1217} = \{1, 3, 5\}\) (these subjects’ outcome times are greater or equal to \(\tau = 1217\) so they are at risk for the event at this time)
- \(n_{\tau = 1217} = |\mathcal{R}_{1217}| = 3\)
- \(d_{\tau = 1217} = 1\): As only \(i = 1\) experienced the event (and not censoring) at this time.
tumor (Bender and Scheipl 2018) time-to-event dataset. Rows are individual observations (ID), \(\mathbf{x}_{;j}\) columns are features, \(t\) is observed time-to-event, \(\delta\) is the event indicator.
| id (\(i\)) | age \((\mathbf{x}_{;1})\) | sex \((\mathbf{x}_{;2})\) | complications \((\mathbf{x}_{;3})\) | days (\(\mathbf{t}\)) | status (\(\boldsymbol{\delta}\)) |
|---|---|---|---|---|---|
| 1 | 71 | female | no | 1217 | 1 |
| 2 | 70 | male | no | 519 | 0 |
| 3 | 67 | female | yes | 2414 | 0 |
| 4 | 58 | male | no | 397 | 1 |
| 5 | 39 | female | yes | 1217 | 0 |
| 6 | 59 | female | no | 268 | 1 |
3.3 Types of Censoring
Three types of censoring are commonly defined in survival analysis: right-censoring, left-censoring, and interval-censoring. The latter can be viewed as the most general case. Multiple types of censoring and/or truncation (Section 3.4) can occur in any given data set and it is vital to identify which types are present in order to correctly select and specify models and measures for the data.
3.3.1 Right-censoring
Right-censoring is the most commonly assumed form of censoring in survival data. It occurs when the event of interest was not experienced during the observation period, which may happen because it was no longer observable (for example, due to withdrawal from the study) or because the event did not happen until study end. The exact event time is unknown but it is known that the event is after the observed censoring time, hence right-censoring (imagine a timeline from left to right as in Figure 3.1).
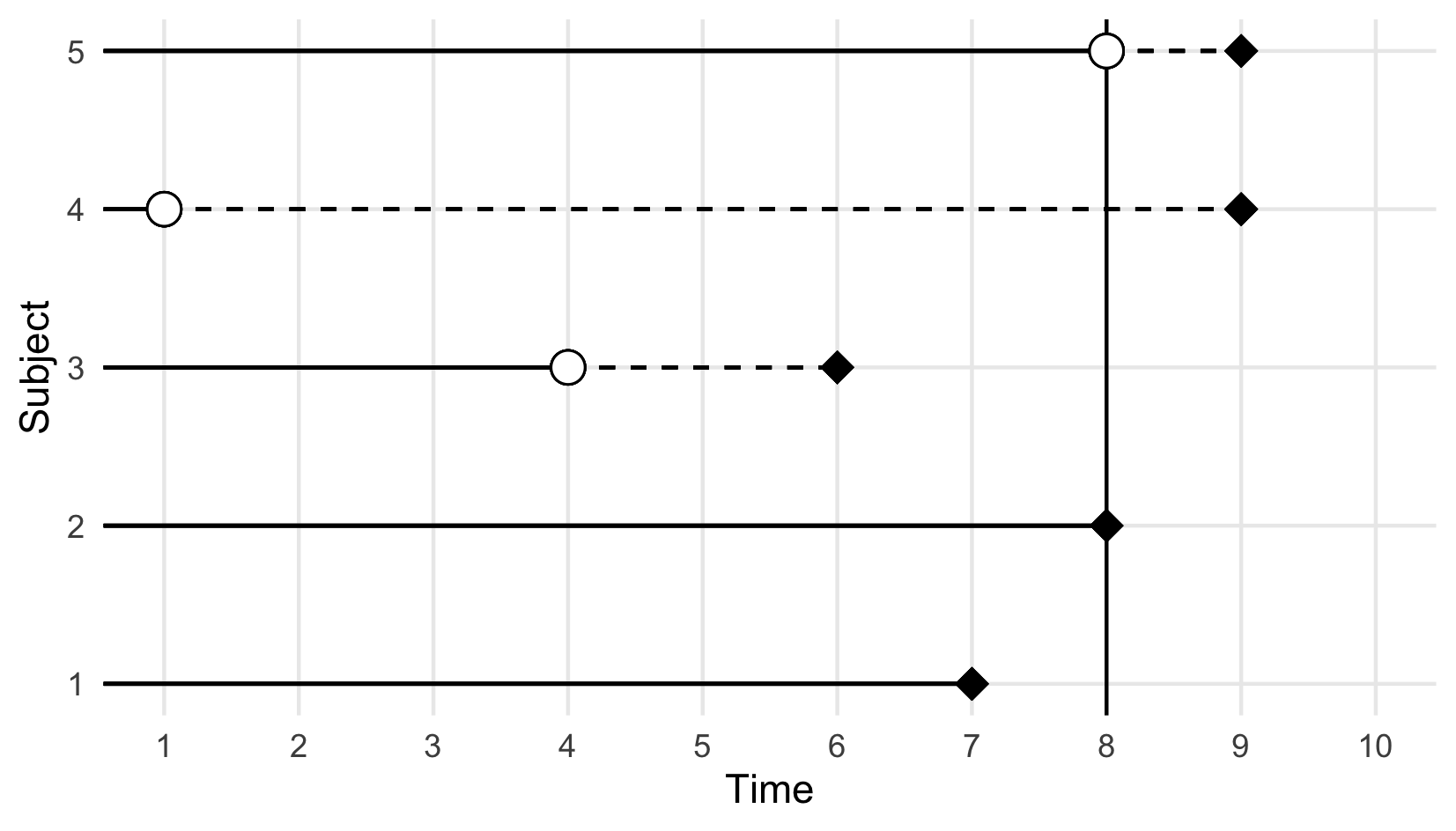
Right-censoring can be further divided into Type-I, Type-II and random censoring. Type-I, or administrative, censoring occurs at the fixed, pre-defined end of an observation period \(\tau_u\), in which case the outcome is given by \((T_i = \min(Y_i, \tau_u), \Delta_i = \mathbb{I}(Y_i \leq \tau_u))\). Censored observations are therefore represented as \((\tau_u, 0)\). Type-II censoring also occurs when the observation period ends. However, in this case the study ends when a pre-defined number of subjects experienced the event of interest and hence \(\tau_u\) is random.
Random censoring occurs when censoring times randomly follow an unknown distribution and one observes \((T_i=\min(Y_i,C_i), \Delta_i = \mathbb{I}(Y_i\leq C_i))\). Different types of right-censoring can, and sometimes do, co-occur in any given data set.
In practice, these different types of right-censoring are usually handled the same during modeling and evaluation and so this book refers to ‘right-censoring’ generally, which could occur from a combination of the above types.
3.3.2 Left- and Interval-censoring
Left-censoring occurs when the event is known to have happened at some unknown time before observation time, interval-censoring occurs when the event is known to have happened within some time span, but not the exact time.
Consider a survey about phone use where participants are asked: “How old were you when you used a smart phone for the first time?”. The possible answers are:
- exact age of first use
- didn’t use a smart phone yet
- did or does use a phone but doesn’t remember age of first time use
- did or does use a phone, remembers a specific age range
The first case represents an exactly observed event time, the second case the familiar right-censoring, as the event may occur later in life, but it is unknown when. The third case is referred to as left-censoring, we know the event occurred before the interview, but don’t know when. The fourth case is an example of interval-censoring, as we know the event occurred within some age span, but not the exact age.
Interval- and left-censoring often occur in medical contexts. For example, some guidelines suggest annual screenings for skin cancer (starting from a certain age). However, the initial age at which individuals do screenings and regularity of check ups varies widely. If cancer was detected between two screenings, the observation is interval-censored. If cancer is detected at first screening, the observation is left-censored (unless the ‘age’ of the cancer can be narrowed down based on size and other characteristics, in which case it would become interval-censored). Also of note, particularly in a medical context, is that interval censoring may be safely ignored depending on the time scale being modelled. Say a patient is screened in February and March 2025 and cancer is detected in the second screening, then they are technically interval censored as (February 2025, March 2025). However, if this data is modelled at an annual scale, then their outcome is known to be [2025] and they are not considered censored.
Censoring Notation
In the presence of left- or interval-censoring the usual representation of survival outcomes as \((t_i, \delta_i)\) is not sufficient to denote the different types of observations in the data set. Instead, we represent the data as intervals in which the event occurs. Formally, let \(Y_i\) the random variable for time until the event of interest and \(L_i, R_i\) random variables that define an interval \((L_i,R_i]\) with realizations \(l_i, r_i\). Let further \(t_i\) the time of observation (for example age at interview in the phone use example) or last-follow up time for subject \(i\). Then the event time of subject \(i\) is
- left-censored if \(Y_i \in (L_i = 0, R_i = t_i]\);
- right-censored at \(t_i\) if \(Y_i \in (L_i = t_i, R_i = \infty)\);
- interval-censored \(Y_i \in (L_i = l_i, R_i = r_i]\), \(l_i < r_i \leq t_i\)
- exactly observed if \(Y_i \in (L_i = t_i, R_i = t_i]\)
In the cancer screening example from above it holds that \(r_i=t_i\) and \(l_i\) the last check-up before \(r_i\). In the phone use example, the participants might specify any age range between \(0\) and \(t_i\).
To make this more concrete, consider phone use example data, where \(t_i\) is the age at interview. In practice, such data is often stored by creating two variables representing the left (\(l_i\)) and right border (\(r_i\)) of the respective intervals (\(t_i\) is not really needed here to define the outcome, but included for illustration).
| id | \(t_i\) | \(l_i\) | \(r_i\) |
|---|---|---|---|
| 1 | 13 | 13 | \(\infty\) |
| 2 | 17 | 15 | 15 |
| 3 | 16 | 14 | 16 |
| 4 | 16 | 13 | 15 |
| 5 | 18 | 0 | 18 |
Here, the first subject is right-censored at 13 years (\(l_i=t_i = 13, r_i = \infty\)), the second subject remembered exactly (\(l_i=r_i=15 < t_i = 17\)), the third subject remembers that it was after 14, but not exact age (\(l_i = 14 < r_i = 16=t_i\)), fourth subject remembers use after 13 years and latest at 15 years of age (\(l_i = 13 < r_i = 15 < t_i\)), and the fifth subject uses a smart phone currently at age 18, but cannot specify further (\(l_i = 0 < r_i = 18 = t_i\)).
From the example above, it is clear, that right- and left-censoring are special cases of interval-censoring. However, if only right- or left-censoring is present, the likelihood and estimation simplifies (see Section 3.5). Also note that in case of left- and interval-censoring the event is known to have occurred, while for right-censoring the event didn’t occur during time under observation. For left- and right-censoring one might be tempted to consider it an event \(\delta_i = 1\) without exact time, while right-censoring would be consider a non-event \(\delta_i = 0\). However, technically it is assumed that the event will always occur, if we wait long enough (for right-censored data in the interval \((t_i, \infty]\)). Censoring therefore means having imprecise information about the time of event rather than information about the event occurring or not occurring.
Dependent vs. Informative Censoring
Censoring may be defined as uninformative if \(Y \perp \!\!\! \perp C\) and informative otherwise. However, these definitions can be misleading as the term ‘uninformative’ could imply that \(C\) is independent of both \(X\) and \(Y\), and not just \(Y\). To avoid misinterpretation, the following definitions are used in this book:
- If \(C \perp \!\!\! \perp X\), censoring is feature-independent, otherwise censoring is feature-dependent.
- If \(C \perp \!\!\! \perp Y\), censoring is event-independent, otherwise censoring is event-dependent.
- If \((C \perp \!\!\! \perp Y) | X\), censoring is conditionally independent of the event given covariates, or conditionally event-independent.
- If \(C \perp \!\!\! \perp(X,Y)\), censoring is uninformative, otherwise censoring is informative.
Uninformative censoring can generally be well-handled by models as the true underlying distribution of survival times is not affected by censoring. In fact, in this case one could even use regression models after removing censored observations (if they do not form a high proportion of the data).
In reality, censoring is rarely non-informative as reasons for drop-out or missingness in outcomes tend to be related to the study of interest. Event-dependent censoring is a tricky case that, if not handled appropriately (by a competing-risks framework), can easily lead to poor model development. Imagine a study is interested in predicting the time between relapses of stroke but a patient suffers a brain aneurysm due to some separate neurological condition. There is a high possibility that a stroke may have occurred if the aneurysm had not. A survival model is unlikely to distinguish the censoring event (aneurysm) from the event of interest (stroke) and will confuse predictions.
In practice, the majority of models and measures assume that censoring is conditionally event-independent and hence censoring patterns can be predicted/estimated based on the covariates. For example, if studying the survival time of ill pregnant patients in hospital, then dropping out of the study due to pregnancy is clearly dependent on how many weeks pregnant the patient is when the study starts (for the sake of argument assume no early/late pregnancy due to illness).
3.4 Censoring vs. Truncation
A common confusion is to conflate censoring and truncation, which is problematic as the methods to handle them differ substantially. Outside of time-to-event settings, truncation usually refers to truncating (or removing) an entire subject from a dataset. As discussed in Chapter 1, truncation in survival analysis refers to partially truncating a period of time and is quite common in the more general event history setting (Chapter 4).
While censored observations have incomplete information about the time-to-event, they are still part of the data set. Whereas truncation leads to observations not entering the data set (at least not at time 0). This will usually introduce bias that needs to be accounted for.
3.4.1 Left-truncation
Left-truncation often occurs when inclusion into a study is conditional on the occurrence of another event. Left-truncation plays an important role when modeling recurrent events or multi-state data (Chapter 4), thus the concept will be introduced in more detail.
By example, consider a study from the 18th century (Broström 1987), when childhood and maternal mortality were relatively high. The goal of the study was to establish the effect of a mother’s death on the survival of the infant. Since each death was reported to the authorities, an infant was added to the study if and when their mother died. To create a matched cohort, two other infants, whose mothers were alive, were matched into the study based on their age and other relevant features. Thus, groups of three infants within the study had identical features except for the status of the mother (alive or dead). Because of the study design, infants who died before their mothers could never enter into the study. A mother’s death is thus referred to as left-truncation event and the infant’s age at time of inclusion into the study is referred to as left-truncation time.
More formally, let \(t^L_i\) the subject-specific left-truncation time. Then we only observe subjects with \(y_i > t^L_i\) and subjects with \(y_i < t^L_i\) never enter the data.
This is illustrated in Figure 3.2. Continuing with the example above, say Infant 1 dies at \(t_1\), while the mother dies at some later time point \(t_1^L\), therefore infant 1 never enters the study. The mother of Infant 2 dies at \(t_2^L\), at which point the infant is included in the study and experiences an event at \(t_2\). Finally, say Infant 3 enters the study at \(t_3^L\) and is censored at 365 days when the study ends.

In this example, left-truncation biases the sample towards healthier or more robust infants, as frail infants on die earlier and thus on average before their mothers. This would bias the estimates if not properly taken into account (see Section 3.5.2.3).
3.4.2 Right-truncation
Right-truncation often occurs in retrospective sampling based on registry data, when data is queried for cases reported by a certain cut-off time (see for example Vakulenko-Lagun, Mandel, and Betensky (2020)). A common example is the estimation of the incubation period of an infectious disease, which is the time from infection to the disease onset. Only known, symptomatic (and/or tested) cases are entered into the database. At a time \(\tau\), one can only observe the subset of the infected population that has already experienced the disease, and not the population that is still incubating the disease, hence biasing the data to shorter incubation periods.
Formally, let \(t_i^r\) be the right-truncation time (here time from infection until the time at which the database is queried), then subjects only enter the data set when \(t_i < t_i^r\). This is illustrated in Figure 3.3 using three subjects. All three subjects were infected during the observation period, however, the right-truncation time \(t_2^r\) of subject 2 is shorter than the incubation period \(t_2\) for this subject, thus at the time of querying the data base, this subject will not be included in the sample, as \(t_2 > t_2^r\).
Note the difference to right-censoring. If subject 2 was right-censored, the subject would be in our sample and the time of infection would be known - the time of disease onset would be censored. In case of right-truncation on the other hand, the subject is not included in the sample at time of data extraction, as subjects are only included in the registry after disease onset. Overall this leads to a bias towards shorter incubation times and potentially feature values that lead to shorter incubation times.

As for left-truncation, ignoring right-truncation will lead to biased estimations. While for left-truncated data simple adjustments of the risk set work for non- and semi-parametric methods like the Kaplan-Meier and Cox-type estimators, this is not the case for right-truncated data. However, parametric methods can be employed (see Section 3.5) and generalised product limit estimators for right-truncated data exist (Akritas and LaValley 2005).
3.5 Estimation
While details about estimation will be given later, when different models are introduced in Part III and Part IV of the book, it is worthwhile discussing some general concepts here, namely parametric and non-parametric approaches.
3.5.1 Parametric estimation
Consider for now uncensored data \((t_i, \delta_i=1), i=1,\ldots,n\). A standard approach would be to assume a suitable distribution for the event times \(t_i \stackrel{iid}{\sim} F_Y(\boldsymbol{\theta}), \boldsymbol{\theta}=(\theta_1,\theta_2,\ldots)^\top\), and define the likelihood of the data as \[ \mathcal{L}(\boldsymbol{\theta}) = \prod_{i=1}^{n}f_Y(t_i|\boldsymbol{\theta}) \tag{3.11}\]
where \(f_Y\) is the pdf of \(F_Y\).
The model parameters can then be obtained by maximizing the likelihood such that
\[ \hat{\boldsymbol{\theta}} = \mathop{\mathrm{arg\,max}}_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta}) \]
However, in the presence of censoring 3.11 is incorrect, as the exact event time is only known for some subjects. For example, for right-censored data (\(\delta_i = 0\)) we only know that the event occurred after observed censoring time \(t_i\). Thus the likelihood contribution for such data points is \(P(Y_i > t_i) = S_Y(t_i)\), whereas for observed event times (\(\delta_i=0\)) the likelihood contribution is \(f_Y(t_i)\) as before.
Let now \(\mathcal{O}= \{i:\delta_i = 1\}\) the index set of observed event times and \(\mathcal{RC} = \{i:\delta_i = 0\}\) the index set of censored observations. The likelihood of this data can be written as
\[ \begin{aligned} \mathcal{L}(\boldsymbol{\theta}) & \propto \prod_{i \in \mathcal{O}}f_Y(t_i|\boldsymbol{\theta})\prod_{i \in \mathcal{RC}}S_Y(t_i|\boldsymbol{\theta})\nonumber\\ & = \prod_{i=1}^n f_y(t_i|\boldsymbol{\theta})^{\delta_i}S_Y(t_i|\boldsymbol{\theta})^{1-\delta_i}\\ & = \prod_{i=1}^n \frac{f_y(t_i|\boldsymbol{\theta})^{\delta_i}}{S_Y(t_i|\boldsymbol{\theta})^{\delta_i}}S_Y(t_i|\boldsymbol{\theta})\\ & = \prod_{i=1}^n h_Y(t_i|\boldsymbol{\theta})^{\delta_i}S_Y(t_i|\boldsymbol{\theta})\nonumber, \end{aligned} \tag{3.12}\]
where the last equality follows from 3.2.
Similar adjustments to the likelihood can be made for other types of censoring and in the presence of truncation. Following Klein and Moeschberger (2003), we can define the individual likelihood contributions for the different types of censoring as
- observed event at \(t_i\): \(f_Y(t_i|\boldsymbol{\theta})\)
- right-censoring: \(P(Y_i > t_i|\boldsymbol{\theta}) = S_Y(t_i|\boldsymbol{\theta})\)
- left-censoring: \(P(Y_i < t_i|\boldsymbol{\theta}) = F_Y(t_i|\boldsymbol{\theta}) = 1 - S_Y(t_i|\boldsymbol{\theta})\)
- interval-censoring: \(P(l_i < Y_i \leq r_i|\boldsymbol{\theta}) = S_Y(l_i|\boldsymbol{\theta}) - S_Y(r_i|\boldsymbol{\theta})\)
Depending on which of the above contributions occur in the data set, we can now construct our likelihood accordingly. Let \(\mathcal{O}, \mathcal{RC}, \mathcal{LC}, \mathcal{IC}\) non-overlapping subsets of the observed data \(\mathcal{D}\) for subjects with observed event times, right-censoring, left-censoring and interval-censoring, respectively. Assuming independence between observations and in absence of truncation, the likelihood for the observed data can be defined as
\[ \mathcal{L}(\boldsymbol{\theta}) \propto \prod_{i \in \mathcal{O}}f_Y(t_i|\boldsymbol{\theta}) \prod_{i \in \mathcal{RC}}S_Y(t_i|\boldsymbol{\theta}) \prod_{i \in \mathcal{LC}}(1-S_Y(t_i|\boldsymbol{\theta}))\prod_{i \in \mathcal{IC}}(S_Y(l_i|\boldsymbol{\theta})-S_Y(r_i|\boldsymbol{\theta})) \tag{3.13}\]
In case of truncation, the adjustments are made to all observations, as we have to condition on the event occurring after/before the truncation time. The truncation adjusted likelihood contributions (assuming independence of truncation and event/censoring times) would thus be given by
left-truncation:
- event: \(f(Y_i = t_i|Y_i \geq t_i^L, \boldsymbol{\theta}) = \frac{f_Y(t_i|\boldsymbol{\theta})}{S_Y(t_i^L|\boldsymbol{\theta})}\)
- left-censoring: \(P(Y_i < t_i|Y_i \geq t_i^L, \boldsymbol{\theta}) = \frac{S_Y(t_i|\boldsymbol{\theta})}{S_Y(t_i^L|\boldsymbol{\theta})}\)
- interval-censoring: \(P(l_i < Y_i \leq r_i|Y_i \geq t_i^L,\boldsymbol{\theta}) = \frac{S_Y(l_i|\boldsymbol{\theta}) - S_Y(r_i|\boldsymbol{\theta})}{S_Y(t_i^L|\boldsymbol{\theta})}\)
right-truncation:
- event: \(f(Y_i = t_i|Y_i \leq t_i^R, \boldsymbol{\theta}) = \frac{f_Y(t_i|\boldsymbol{\theta})}{F_Y(t_i^R|\boldsymbol{\theta})}\)
- left-censoring: \(P(Y_i < t_i|Y_i \leq t_i^R, \boldsymbol{\theta}) = \frac{S_Y(t_i|\boldsymbol{\theta})}{F_Y(t_i^R|\boldsymbol{\theta})}\)
- interval-censoring: \(P(l_i < Y_i \leq r_i|Y_i \leq t_i^R,\boldsymbol{\theta}) = \frac{S_Y(l_i|\boldsymbol{\theta}) - S_Y(r_i|\boldsymbol{\theta})}{F_Y(t_i^R|\boldsymbol{\theta})}\)
Note that in in practice, data sets will often not contain all types of censoring or truncation, in which case 3.13 will contain only a subset of the product terms. This has been illustrated in 3.12 under absence of truncation and \(\mathcal{LC}=\mathcal{IC}=\emptyset\).
3.5.2 Non-parametric estimation
As the name suggests, non-parametric estimation (and semi-parametric estimation) techniques do not make (strong) assumptions about the underlying distribution of event times.
A common principle for such techniques is to partition the follow-up into intervals (or to define specific time-points during the follow-up) and to estimate the continuous (3.2) or discrete time (3.5) hazards for each interval/time-point. Once the respective hazard estimates are obtained, estimates of other quantities, for example the survival probability, can be derived based on the relationship given in Section 3.1.1 or Section 3.1.2.
3.5.2.1 Kaplan-Meier estimator
The Kaplan-Meier estimator (Kaplan and Meier 1958), a simple, non-parametric estimator for the survival function (3.1), is an example for this principle. While it is usually used for continuous time, its construction can be motivated from a discrete time persepective. Recall from Section 3.2 the definition of unique, ordered, event time \(t_{(k)}, k=1,\ldots,m\) (3.9). Define \(\tilde{Y} = t_{(k)} \Leftrightarrow Y \in (t_{(k-1)},t_{(k)}]\) as discrete time representation of \(Y\). Using the quantities introduced in Section 3.2,the discrete time hazard 3.5 is estimated as the ratio of the number of events occurring at \(t_{(k)}\), to the number of subjects at risk at \(t_{(k)}\):
\[ h^d(t_{(k)}) = P\left(Y\in (t_{(k-1)},t_{(k)}]|Y>t_{(k-1)}\right)=\frac{d_{t_{(k)}}}{n_{t_{(k)}}}. \tag{3.14}\] The survival probability and the definition of the Kaplan-Meier estimator (3.15) then follow from 3.7: \[ S(\tau) = \prod_{k:t_{(k)} \leq \tau}\left(1-\frac{d_{t_{(k)}}}{n_{t_{(k)}}}\right) \tag{3.15}\]
which is a step-function at the observed ordered event times \(t_{(k)}, k=1,\ldots,m\) with \(S_{KM}(\tau) = 1\ \forall \tau < t_{(1)}\). It is usually estimated for all unique event times. In this book, \(\hat{S}_{KM}\) specifically refers to the Kaplan-Meier estimator fit on some training data.
For illustration, we consider the tumor data set from Section 3.2. Figure 3.4 shows the estimated survival probability obtained by applying the Kaplan-Meier estimator to the full data set, containing observations of \(n=776\) subjects. By definition, the survival function starts at \(S(t)=1\) at \(t=0\) and monotonically decreases towards \(S(t)=0\) for \(t\rightarrow \infty\). However, follow-ups are usually not infinite and in the presence of censoring, the survival function may not reach 0 by the end of the observation period. For the Kaplan-Meier estimator specifically, \(\hat{S}_{KM}(t_{(m)}) = 0\) only if the last observed time is an event time and there are no censored observations at the same time.
Dotted lines indicate the median survival, defined as the time at which the survival function reaches \(S(t) = 0.5\). In this example, the median survival time is approximately 1500 days. This means that 50% of the subjects are expected die within 1500 days after operation.
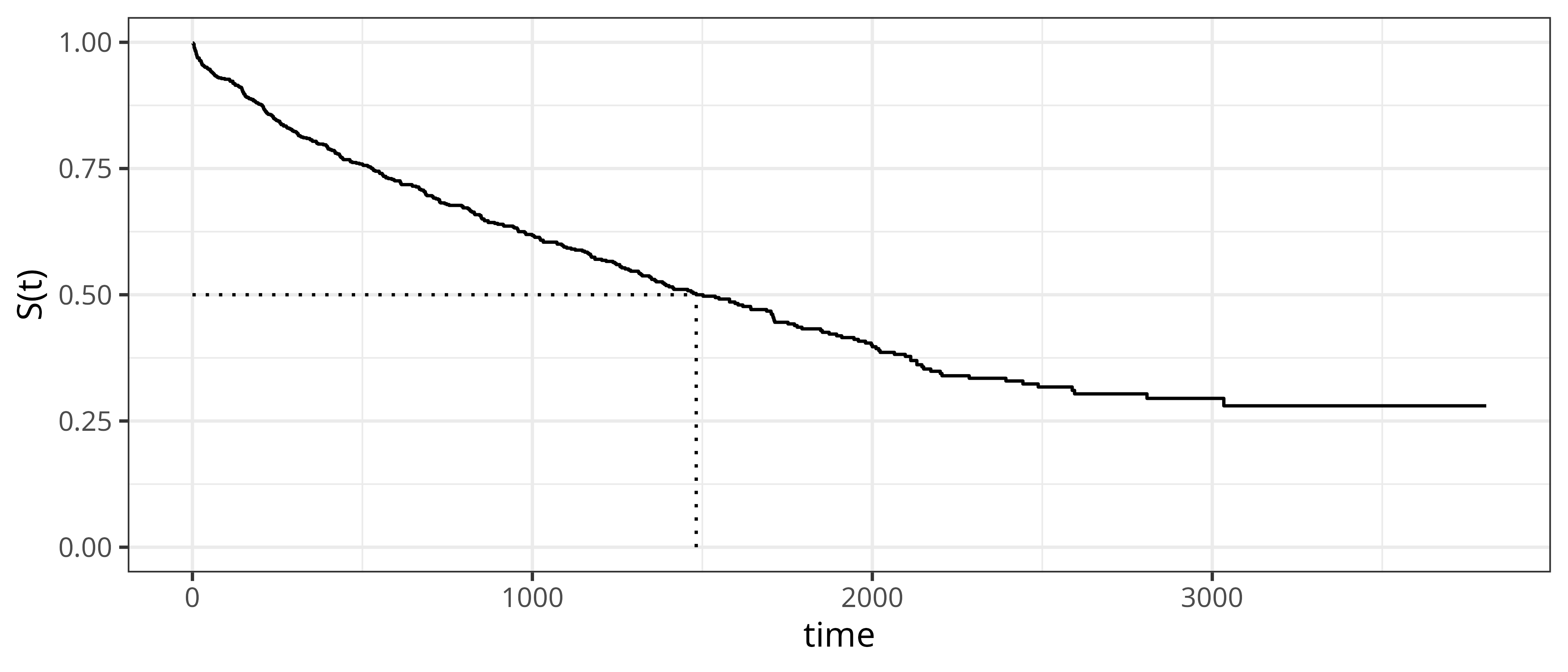
tumor data (Bender and Scheipl 2018). The estimated survival probabilities are given by the solid step-function. Dotted lines indicate the median survival time).
While the Kaplan-Meier estimator does not directly support estimation of covariate effects on the estimated survival probabilities, it is often used for descriptive analysis by applying the estimator to different subgroups (referred to as stratification in survival analysis). For example, Figure 3.5 shows \(\hat{S}_{KM}\) separately for subjects aged 50 years or older and subjects younger than 50 years, respectively. Dashed lines again illustrate median survival times. However, note that the median survival time does not exist for the younger age group, as their estimated survival function does not cross \(0.5\).
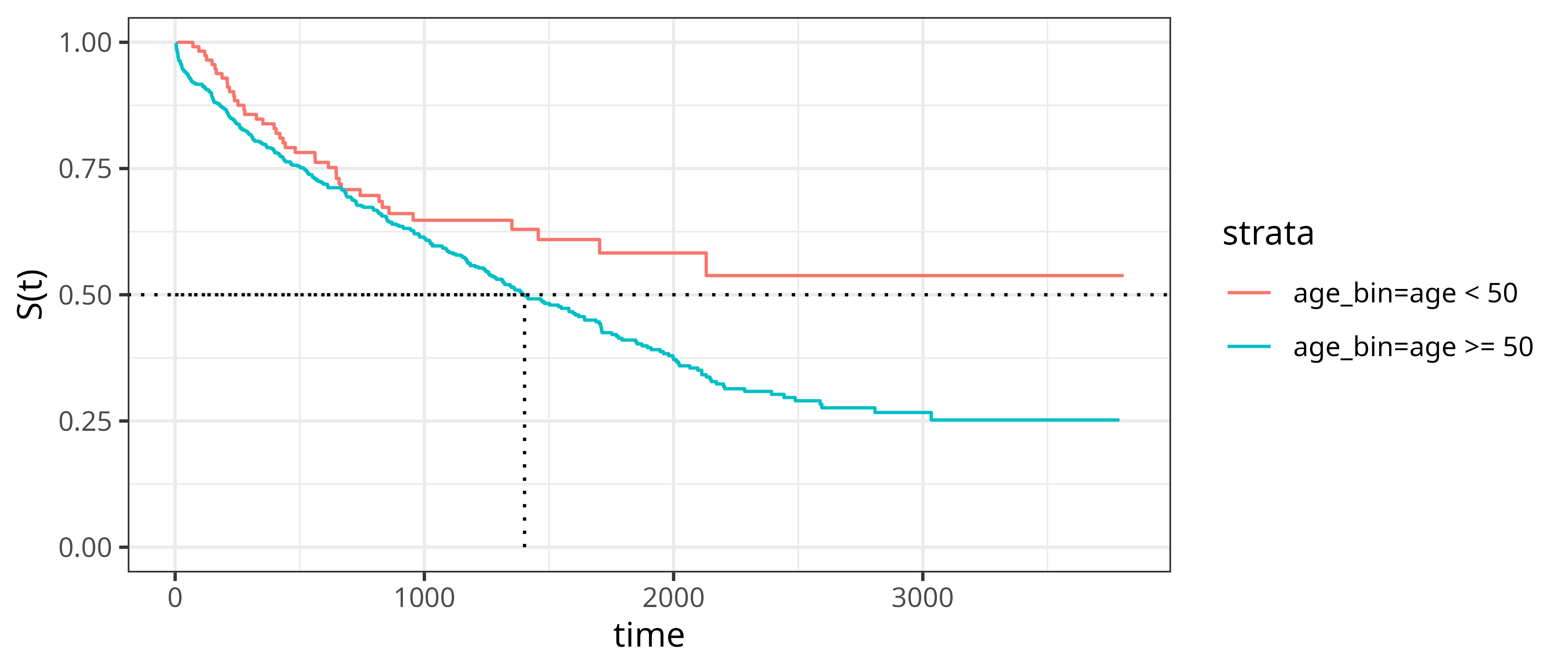
tumor data (Bender and Scheipl 2018) applied to subgroups of subjects of 50 or more years old and less than 50 years old, respectively. The estimated survival probabilities are given by the solid step-function. Dotted lines indicate the median survival time).
3.5.2.2 Nelson-Aalen
As the Kaplan-Meier estimator (Section 3.5.2.1), the Nelson-Aalen estimator (Nelson (1972),Aalen (1978)) is based on the discrete time hazards 3.14. Rather than estimating the survival probability, the Nelson-Aalen estimator estimates the discrete time cumulative hazard function 3.6 and is defined as
\[ H_{NA}(\tau) = \sum_{k:t_{(k)}\leq \tau} h^d(t_{(k)}) = \sum_{k:t_{(k)}\leq \tau} \frac{d_{t_{(k)}}}{n_{t_{(k)}}}. \tag{3.16}\]
Note that we use a continuous time valued \(\tau\) for the definition, which implies that \(H_{NA,e}(\tau) = H_{NA,e}(t_{(k)})\ \forall \tau \in [t_{(k)}, t_{(k+1)})\). In words: For time points between two unique event times we assume the previous value of the estimate.
Based on 3.4 we can also define a survival probability estimator based on the Nelson-Aalen estimator as
\[ S_{NA}(\tau) = \exp(-H_{NA}(\tau)). \tag{3.17}\]
Kaplan–Meier and Nelson–Aalen are consistent for survival and cumulative hazard respectively under independent right-censoring. Both these non-parametric estimators can be used as simple predictive methods (Section 10.1), and are often used as informative baseline models, which can be compared to sophisticated alternatives to improve interpretability in model evaluation (Herrmann et al. 2021; Huang et al. 2020; Wang, Li, and Reddy 2019). Both methods can also be used for graphical calibration of models (Section 7.2.1), components of complex models (Chapter 15), and other diagnostic graphical tools (Habibi et al. 2018; Jager et al. 2008; Moghimi-dehkordi et al. 2008).
3.5.2.3 Left truncation
Non-and semi-parametric estimators can be easily extended to deal with left-truncation by adjusting the risk set definition (3.10) to the more general definition (McGough et al. 2021) \[ \mathcal{R}_\tau^L = \{i: t_i^L \ \leq \tau \leq t_i \}, \tag{3.18}\] which excludes individuals from the risk set until their left-truncation time has occurred (3.18).
The number of individuals at risk at \(\tau\) is then \[ n^L_\tau = |\mathcal{R}_\tau^L| = \sum_i \mathbb{I}(t_i^L \leq \tau \leq t_i), \tag{3.19}\] where \(t_i, t_i^L\) are the outcome time and left truncation time of observation \(i\) respectively.
The Kaplan-Meier (3.15) and Nelson-Aalen (3.16) estimators can still be used with \(n_{t_{(k)}}\) replaced by \(n^L_{t_{(k)}}\) and \(d_{t_{(k)}}\) calculated in the usual manner.
For illustration consider an excerpt from the infants data in Table 3.2 discussed in Section 3.4.1, where \(t\) is the observed event or censoring time and \(t^L\) is the left-truncation time.
infants (Broström 2024) time-to-event dataset. Rows are individual observations (id), group indicates matched infants, \(t^L\) is the left-truncation time (time of inclusion into the study), \(t\) is the observed time, \(\delta\) is the event indicator.
| group | id | \(t^L\) | \(t\) | \(\delta\) | mother |
|---|---|---|---|---|---|
| 1 | 1 | 55 | 365 | 0 | dead |
| 1 | 2 | 55 | 365 | 0 | alive |
| 1 | 3 | 55 | 365 | 0 | alive |
| 2 | 4 | 13 | 76 | 1 | dead |
| 2 | 5 | 13 | 365 | 0 | alive |
| 2 | 6 | 13 | 365 | 0 | alive |
| 4 | 7 | 2 | 16 | 1 | dead |
| 4 | 8 | 2 | 365 | 0 | alive |
| 4 | 9 | 2 | 365 | 0 | alive |
In Table 3.2, without stratifying according to mother’s status, the first observed event time is \(t_{(1)} = t_7=16\). Then, ignoring left-truncation,
- \(\mathcal{R}_{t_{(1)}} = \{1,2,3,4,5,6,7,8,9\}\)
- \(d_{t_{(1)}} = 1\)
- \(n_{t_{(1)}} = 9\)
- \(S(t_{(1)}) = 1 - \frac{1}{9} \approx 0.9\)
In contrast, when we take left-truncation into account, subjects only enter the risk set for the event after their left-truncation time (we already know they survived until \(t_i^L\) so they are not at risk for the event before that time), thus
- \(\mathcal{R}^L_{t_{(1)}} = \{4, 5, 6, 7, 8, 9\}\)
- \(d_{t_{(1)}} = 1\)
- \(n_{t_{(1)}}^L = 6\)
- \(S(t_{(1)}) = 1 - \frac{1}{6} \approx 0.8\)
Thus, in the presence of left-truncation, \(n_{t_{(k)}}^L \leq n_{t_{(k)}}\) and therefore \(S(t_{(k)})^L \leq S(t_{(k)})\).
Figure 3.6 shows the difference between estimated survival probabilities when left-truncation is ignored (left panel) and taken into account (right panel), respectively. It is clear that the survival probabilities were underestimated in both groups, but more so in the group of infants whose mother died (thereby underestimating the effect of the mothers’ death on infant survival).
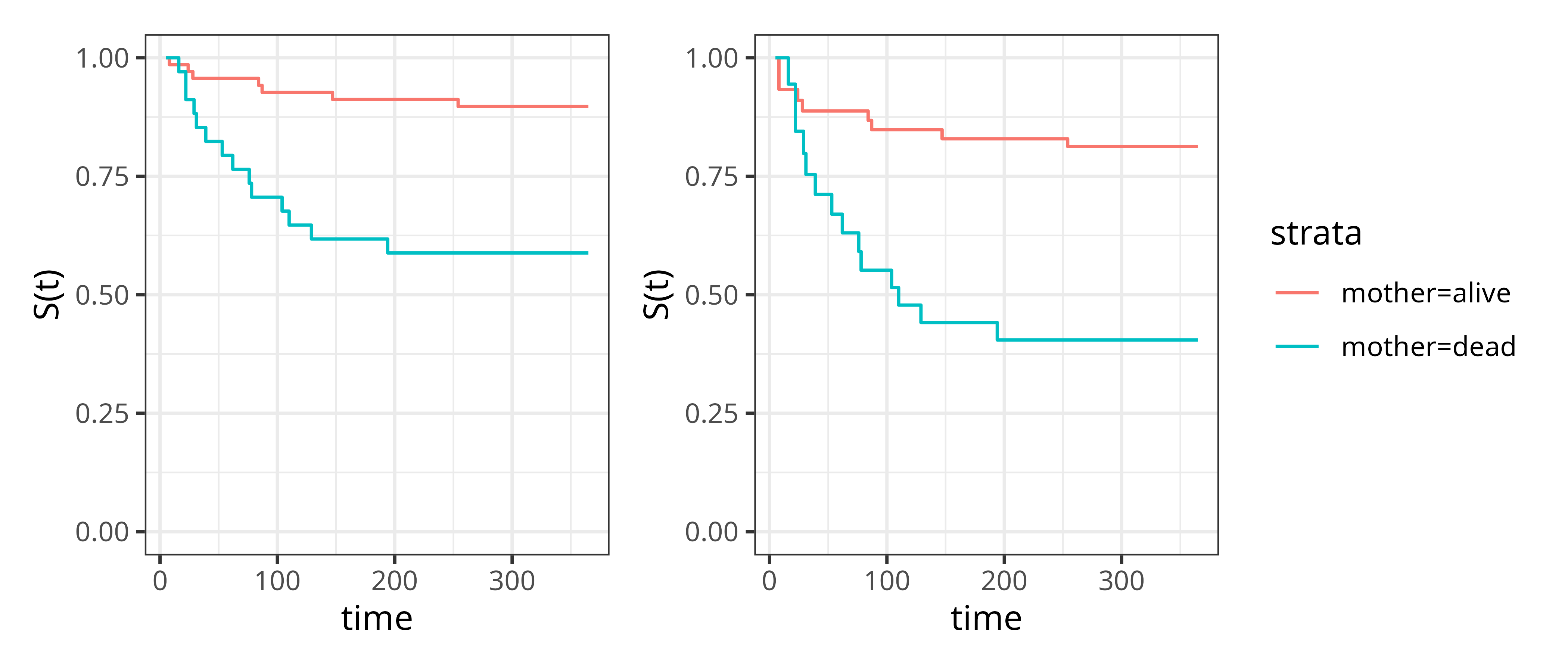
Interval-censoring
For interval-censoring, the Kaplan-Meier estimator is replaced by the nonparametric maximum likelihood estimator (NPMLE) (Zhang and Sun 2010), which estimates the likelihood function under the assumption of left- or interval-censored data as in Section 3.5.1. The most common algorithm to compute this is the iterative Turnbull algorithm (Turnbull 1974). The intuition behind this algorithm is that an observation, \(i\), should only contribute to the estimation at a given time-point, \(\tau\), if the event could have happened in the censoring interval, \(\tau \in (L_i, R_i]\).
In summary (Giolo 2004):
Let \(t_{(k)}, k = 1,...,m\) be the ordered times at which to evaluate the NPMLE.
- Make an initial guess for \(\hat{S}^0(t_{(k)}), k = 1,...,m\).
Where \(\hat{S}^0\) is the initial guess. Let \(\hat{S}^j\) be the estimated survival function at iteration \(j\).
- While \(\quad \lvert \hat{S}^j(t_{(k)}) - \hat{S}^{j-1}(t_{(k)}) \rvert > \epsilon, \forall k = 1,...,m \quad\) Do:
- Compute the probability of an event at each time-point:
\[ p_{t_{(k)}} = \hat{S}^{j-1}(t_{(k-1)}) - \hat{S}^{j-1}(t_{(k)}), \quad k = 1,...,m \]
- Estimate the number of events at each time-point:
\[ d_{t_{(k)}} = \sum^n_{i=1} \frac{w_{ik}p_{t_{(k)}}}{\sum^m_{l=1} w_{il}p_{t_{(l)}}}, \quad k = 1,...,m \]
Where \(w_{ik} = 1\) if the interval \((t_{(k-1)}, t_{(k)}]\) is contained within \((L_i, R_i]\), and \(w_{ik} = 0\) otherwise; and \(L_i, R_i\) are the left- and right-censoring times for observations \(i = 1,...,n\).
- Compute the cumulative number of events at or after \(t_{(k)}\):
\[ n_{t_{(k)}} = \sum^m_{l=k} d_{t_{(l)}}, \quad k = 1,...,m \]
This serves a similar role to the usual ‘number at risk’ formula.
- Calculate \(\hat{S}^j\) using the Kaplan-Meier formula (3.15), substituting the values in Steps 2b and 2c.
Giolo (2004) suggest using the Kaplan-Meier to find the initial guess in Step 1 and to use \(\epsilon = 10^{-3}\). A similar algorithm can be used for left-censored data.
3.6 Estimation of the censoring distribution
The techniques discussed in section Section 3.5 can also be used to estimate the distribution of censoring times \((t_i, 1-\delta_i)\). This is often done in order to calculate the inverse probability of censoring weights (Section 3.6.2) used in the evaluation of survival models (Section 6.1.1) and in order to account for (covariate-)dependent censoring (Willems et al. (2018)).
3.6.1 The Kaplan-Meier estimator for the censoring distribution
The Kaplan-Meier estimator can be used to estimate the distribution of censoring times. The definition of the risk set (3.10) is thus the denominator \(n_{\tau}\) in 3.14 remains the same, but the numerator \(d_{\tau}\) is now the number of censoring events at \(\tau\), which we denote as
\[ d_\tau^C = \sum_i \mathbb{I}(t_i = \tau, \delta_i = 0). \]
The Kaplan-Meier estimator for the censoring distribution is then given by
\[ G_{KM}(\tau) = \prod_{\ell:t_{(\ell)} < \tau} \left(1-\frac{d^C_{t_{(\ell)}}}{n_{t_{(\ell)}}}\right), \tag{3.20}\]
where \(t_{(\ell)},l=1,\ldots,g\) are the unique, ordered censoring times. In this book, \(\hat{G}_{KM}\) specifically refers to the Kaplan-Meier estimator fit to the observed censoring times \((t_i, 1-\delta_i)\) from some training data.
3.6.2 Inverse probability of censoring weights (IPCW)
The inverse probability of censoring (IPC) weights are defined as
\[ w(\tau|\mathbf{x}) = \frac{1}{S(\tau|\mathbf{x})} \tag{3.21}\]
When no relationship between the censoring time and the covariates is assumed, the IPC weights are in most cases estimated by plugging in the Kaplan-Meier estimate of 3.20 into 3.21, such that
\[ \hat{w}(\tau) = \frac{1}{\hat{G}_{KM}(\tau)} \tag{3.22}\]